Download#

Download the most recent draft of Napkin. Or download the cover art image.

You can also see all generated files, including a folder with each individual part.

Project Status#

Following semver, the version number 1.6 indicates the addition of a few new chapters (and many typo fixes), as well as a pretty cover artwork. Nonetheless, there are several chapters scheduled but not yet written, and many chapters still lack problems or solutions.

See link above for the most recent draft. You can also view the source code on GitHub; the most recent version is automatically compiled from that source.

I would highly appreciate any corrections, suggestions, or comments. The best way to propose changes is to submit a pull request on GitHub. Alternatively, for longer discussion or general action items, submit an issue on GitHub.

Description#

An Infinitely Large Napkin is a light and mostly self-contained introduction to higher math, roughly ranging from the undergraduate syllabus to first-year graduate topics. The Napkin provides a general bird’s-eye views of main ideas of fields and what makes them cool or interesting. It’s less detailed than a real textbook but more precise than pop-math books and assumes proof experience. So for example, definitions and theorem statements will typically be complete and precise, but explanations for why a result “should” be true will supersede formal proofs.

PDF’s for individual parts#

You can also see an auto-generated table of contents as text.

You can download the entire PDF. Nonetheless, if you need a per-part PDF, you can use the ones below; though note hyperlinks that span across parts will obviously not work. If you want the figures, check all generated files.

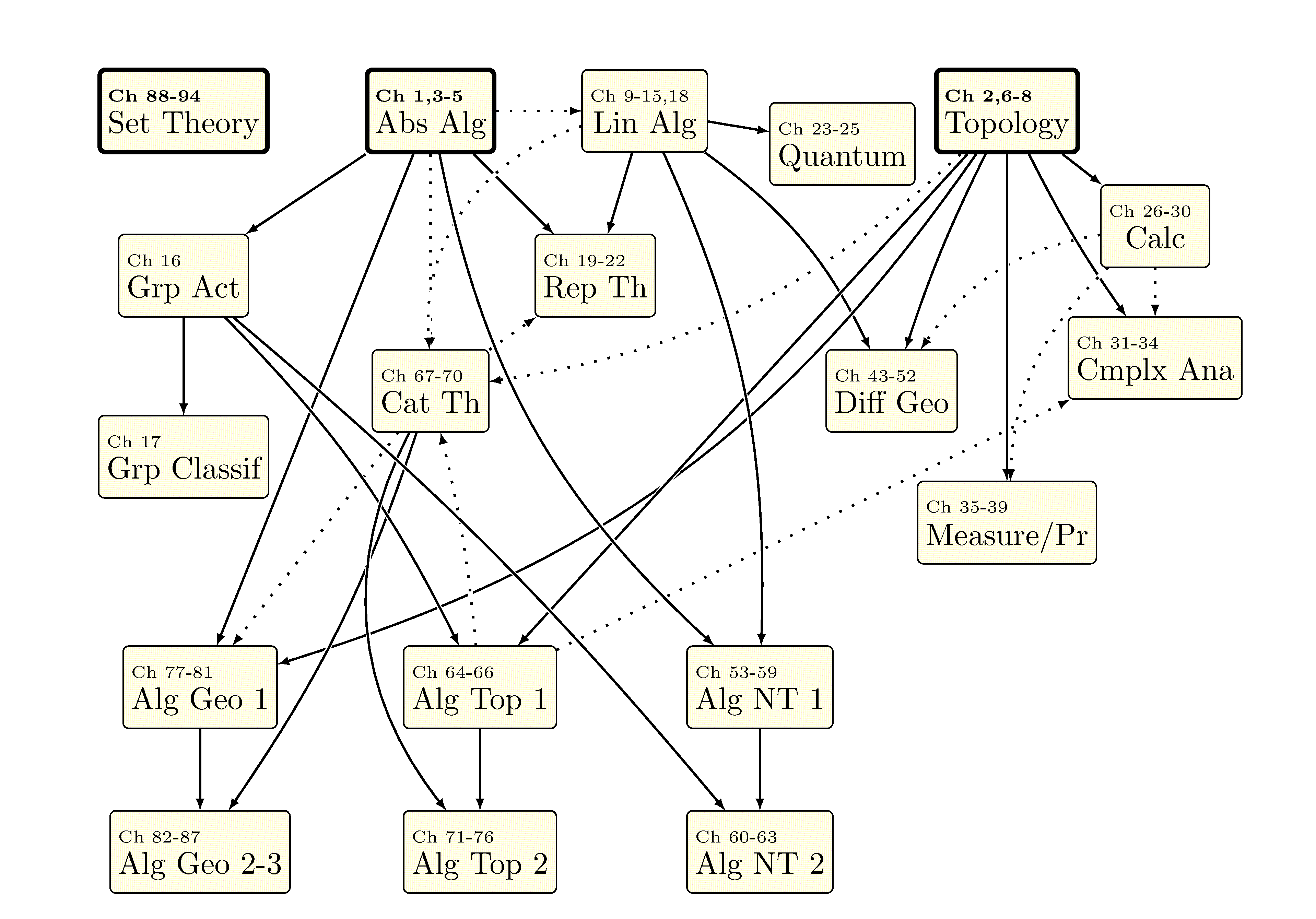
There’s also a flowchart by chapter number (rather than part number).

• Frontmatter

1. Starting Out
2. Basic Abstract Algebra
3. Basic Topology
4. Linear Algebra
5. More on Groups
6. Representation Theory
7. Quantum Algorithms
8. Calculus 101
9. Complex Analysis
10. Measure Theory
11. Probability (TO DO)
12. Differential Geometry
13. Riemann Surfaces
14. Algebraic NT I: Rings of Integers
15. Algebraic NT II: Galois and Ramification Theory
16. Algebraic Topology I: Homotopy
17. Category Theory
18. Algebraic Topology II: Homology
19. Algebraic Geometry I: Classical Varieties
20. Algebraic Geometry II: Affine Schemes
21. Set Theory I: ZFC, Ordinals, and Cardinals
22. Set Theory II: Model Theory and Forcing
23. Appendix

Community solutions#

There is a community working on both human-readable and Lean4 proofs of Napkin problems and examples. See:

• Napkin formal proofs (Lean4): napkin-community/proofs
• Napkin human-readable solutions (Typst): napkin-community/solutions
  • Rendered: napkin-community.github.io/solutions (written in Typst)